rabbit hole
本文最后更新于:2025年5月26日 下午
好像有首叫 ラビットホール 的小黄歌来着
有一个无向联通图 \(G<V,E>\),在某一个点上有一只兔子。从某时刻开始,每个周期你可以选择一个点查看兔子是否在这个点,然后兔子移动到相邻的点(不能停留在原点)。问你是否存在一种查看的顺序能够保证找到兔子。
这个问题也等价于,每个点上有无数只兔子,同样的游戏规则,问你是否能有一种方法找到所有兔子。一只能找到那么所有的当然也可以。反过来所有地方有兔子都能全部找到,那么一只兔子无论开始在哪里都可以找到。
首先我们可以考虑几种特殊的情况。
如果这个图不是树的话,那么一定存在环。如果有环,兔子可以一直沿着环走,不存在一种查看方式能将兔子活动范围限制在某个区域。
\(|G|\) 比较小。这时候可以考虑状压 \(dp\)。状态 \(dp[mask]\) 表示这些点都有无限只兔子的时候,能不能找出所有兔子。转移就枚举看了哪个点,然后剩下的兔子走到相邻节点。
这个图是一条链。

不妨假设兔子最开始在的点为黑点,这就意味着奇数时刻兔子一定在黑点,而偶数时刻兔子在白点。所以我们奇数时刻看黑点,偶数时刻看白点。
从点 \(1\)(黑点) 开始依次看右边的点,这时候兔子如果不在 1 就在右边的点。可以发现,当我们在看 \(i\) 点的时候,兔子不可能出现在更小的点。因为发生交换只有在看某个 \(j\) 点的时候兔子在 \(j + 1\) 处然后下一时刻看 \(j+1\) 兔子在 \(j\)。但是这种情况是不可能的,因为我们看的点一定和兔子所在点颜色相同。
然后因为兔子最开始不一定在黑点,所以要从 \(n\) 开始倒着看一遍,多看一次 \(n\) 刚好交换了奇偶性。
可以从一条链入手考虑更一般的情况,不妨考虑以一条链为基础挂上一些点和边来形成一棵树。直觉为了满足要求,挂的点越少越好。
接下来我们都假设兔子一开始在黑点,从左到右查看。如果是在白点,那么反之亦然。
- 添加一层点
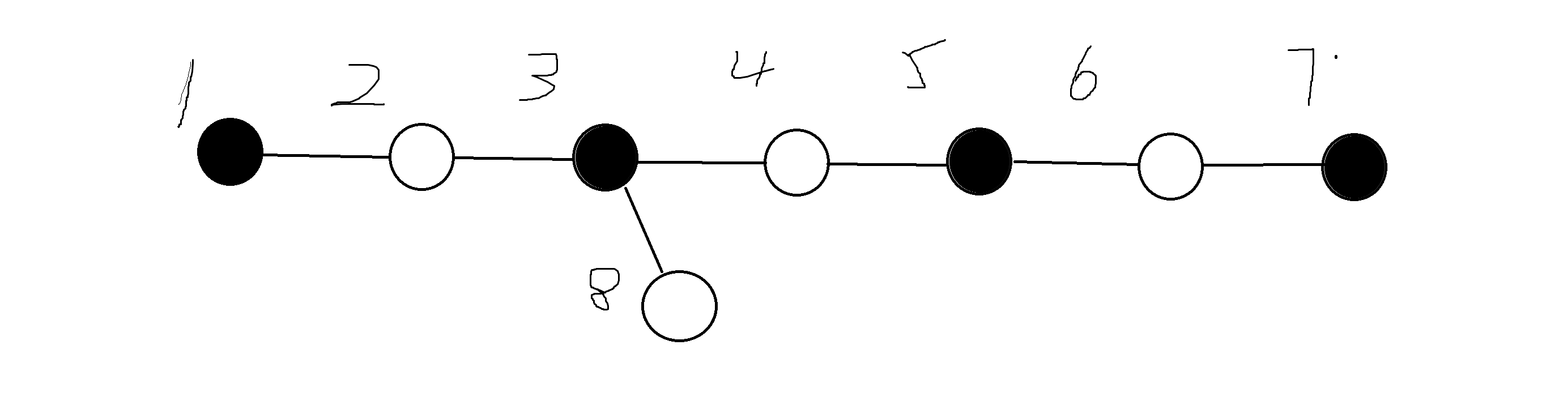
能抓到兔子,也就是说我们在看 \(i\) 点时,兔子还是一定在 \(i\) 右边或者在 \(i\) 点(将挂在链上的点和对应的链上的点看作一个整体)。
这是显然的,因为我们在看 \(i\)(比如点 3) 点的时候,兔子一定不在分支(比如点8)上,因为他们颜色不同。
- 添加两层点
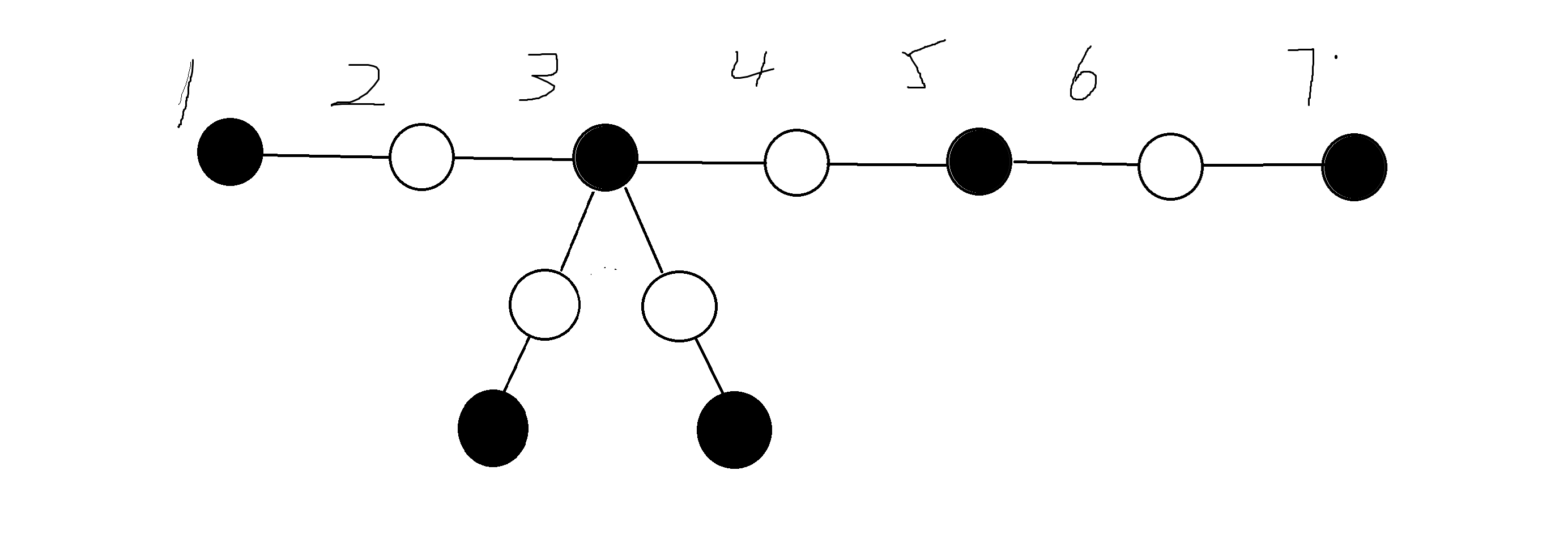
当查看链上对应的点 \(i\)(比如图中点 3) 的时候,兔子一定不会在第一层(原因同上)。但是我们不确定兔子在链上还是子树。这时候我们在奇数时刻都要查看 \(i\),这样做的好处是保证兔子不会从子树溜到外面或者从链的右边溜到左边。空下来的偶数时间依次查看周围的白点。
如果兔子在子树里,因为一定移动,那么兔子会从第二层来到第一层,刚好被发现。如果兔子在链上,那么和一条链的情况一样。
- 添加三层点
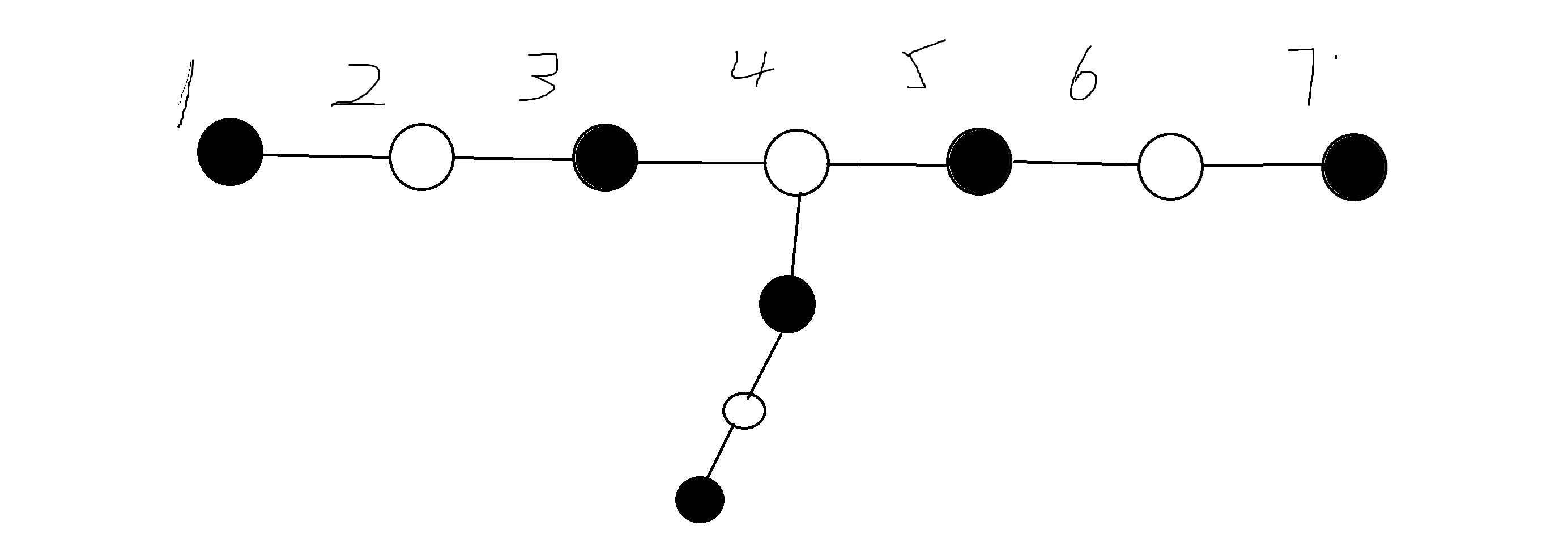
这种情况下,没有办法封锁住点 4,所以不行。
实际上,只要给的图不存在图四这样的子图,就都是合法的。虽然只讨论给一个点上挂点的情况,结合之前的讨论,很容易发现更多的点也是一样的。因为总是可以保证兔子在更右边的点上。
参考: